Calculates a p-value surface based on asymptotic theory or Monte-Carlo (MC) permutations describing the extremity of risk given a fixed or adaptive kernel-smoothed density-ratio, allowing the drawing of tolerance contours.
tolerance(
rs,
method = c("ASY", "MC"),
ref.density = NULL,
beta = 0.025,
ITER = 100,
parallelise = NULL,
verbose = TRUE,
...
)Arguments
- rs
An object of class
rrsgiving the estimated relative risk function for which to calculate the p-value surface.- method
A character string specifying the method of calculation.
"ASY"(default) instructs the function to compute the p-values using asymptotic theory."MC"computes the values by random permutations of the data. See `Details'.- ref.density
Required if
rsis based on fixed-bandwidth estimates of the case and control densities andmethod = "ASY". Either a pixelimage or an object of classbivdengiving the reference density to use in asymptotic formulae. May be unnormalised. Ignored ifrsis based on adaptive kernel estimates or ifmethod = "MC".- beta
A numeric value \(0 <\)
beta\(< 1\) giving the fineness of the adaptive bandwidth partitioning to use for calculation of the required quantities for asymptotic adaptive p-value surfaces. Smaller values provide more accurate bandwidth bins at the cost of additional computing time, see Davies and Baddeley (2018); the default is sensible in most cases. Ignored ifrsis based on fixed-bandwidth kernel estimates.- ITER
Number of iterations for the Monte-Carlo permutations. Ignored if
method = "ASY".- parallelise
Numeric argument to invoke parallel processing, giving the number of CPU cores to use when
method = "MC". Experimental. Test your system first usingparallel::detectCores()to identify the number of cores available to you.- verbose
Logical value indicating whether to print function progress during execution.
- ...
Additional arguments to be passed to
riskwhenmethod = "MC". While most information needed for the MC repetitions is implicitly gleaned from the object passed tors, this ellipsis is typically used to set the appropriateepsilonandpilot.symmetryvalues for the internal calls torisk.
Value
A pixel image of the estimated
p-value surface.
Details
This function implements developments in Hazelton and Davies (2009) (fixed) and Davies and Hazelton (2010) (adaptive) to compute pointwise p-value surfaces based on asymptotic theory of kernel-smoothed relative risk surfaces. Alternatively, the user may elect to calculate the p-value surfaces using Monte-Carlo methods (see Kelsall and Diggle, 1995). Superimposition upon a plot of the risk surface contours of these p-values at given significance levels (i.e. ``tolerance contours'') can be an informative way of exploring the statistical significance of the extremity of risk across the defined study region.
Implementation of the Monte-Carlo method simply involves random allocation of case/control marks and
re-estimation of the risk surface ITER times, against which the
original estimate is compared. While not dependent on asymptotic theory, it is
computationally expensive, and it has been suggested that it might have some
undesirable practical consequences in certain settings (Hazelton and Davies,
2009). When performing the MC simulations, the same global (and pilot, if
necessary) bandwidths and edge-correction regimens are employed as were used
in the initial density estimates of the observed data. With regard to
arguments to be passed to internal calls of risk, the user
should take care to use ... to set the epsilon value to match
that which was used in creation of the object passed to rs (if this
was set to a non-default value). Furthermore, if performing MC simulations
for the adaptive relative risk function, the function borrows the value of
the beta argument to speed things up via partitioning, and the user
should additionally access ... to set the same pilot.symmetry
value as was used for creation of the object passed to rs, in the
same way as for any non-default use of epsilon. This will ensure the
simulations are all performed under the same conditions as were used to estimate the original risk
function.
Note
The returned p-values are geared so that ``smallness''
corresponds to statistical significance of elevated risk, that is, an
upper-tailed test. The complement of the p-values will yeild
significance of reduced risk; a lower-tailed test. When using
tol.contour, the user can control what type of contours to
display.
References
Davies, T.M. and Baddeley A. (2018), Fast computation of spatially adaptive kernel estimates, Statistics and Computing, 28(4), 937-956.
Davies, T.M. and Hazelton, M.L. (2010), Adaptive kernel estimation of spatial relative risk, Statistics in Medicine, 29(23) 2423-2437.
Davies, T.M., Jones, K. and Hazelton, M.L. (2016), Symmetric adaptive smoothing regimens for estimation of the spatial relative risk function, Computational Statistics & Data Analysis, 101, 12-28.
Hazelton, M.L. and Davies, T.M. (2009), Inference based on kernel estimates of the relative risk function in geographical epidemiology, Biometrical Journal, 51(1), 98-109.
Kelsall, J.E. and Diggle, P.J. (1995), Kernel estimation of relative risk, Bernoulli, 1, 3-16.
Examples
# \donttest{
data(pbc)
h0 <- LSCV.risk(pbc,method="hazelton");h0
#> Searching for optimal Hazelton h in [0.1,15.278]...Done.
#> [1] 3.04405
pbccas <- split(pbc)[[1]]
pbccon <- split(pbc)[[2]]
# ASY
riskfix <- risk(pbc,h0=h0)
#> Estimating case and control densities...
#> Done.
fixtol1 <- tolerance(riskfix,ref.density=density(pbc,OS(pbc)))
#> Initialising window...Done.
#> Performing kernel*window convolution(s)...Done.
riskada <- risk(pbc,h0=h0,adapt=TRUE,hp=NS(pbc),pilot.symmetry="pooled",davies.baddeley=0.025)
#> Estimating case density...
#> Done.
#> Estimating control density...
#> Done.
adatol1 <- tolerance(riskada)
#> Initialising window...Done.
#> Convolving bandwidth-categorised kernels with window:
#> --pass 1...Done.
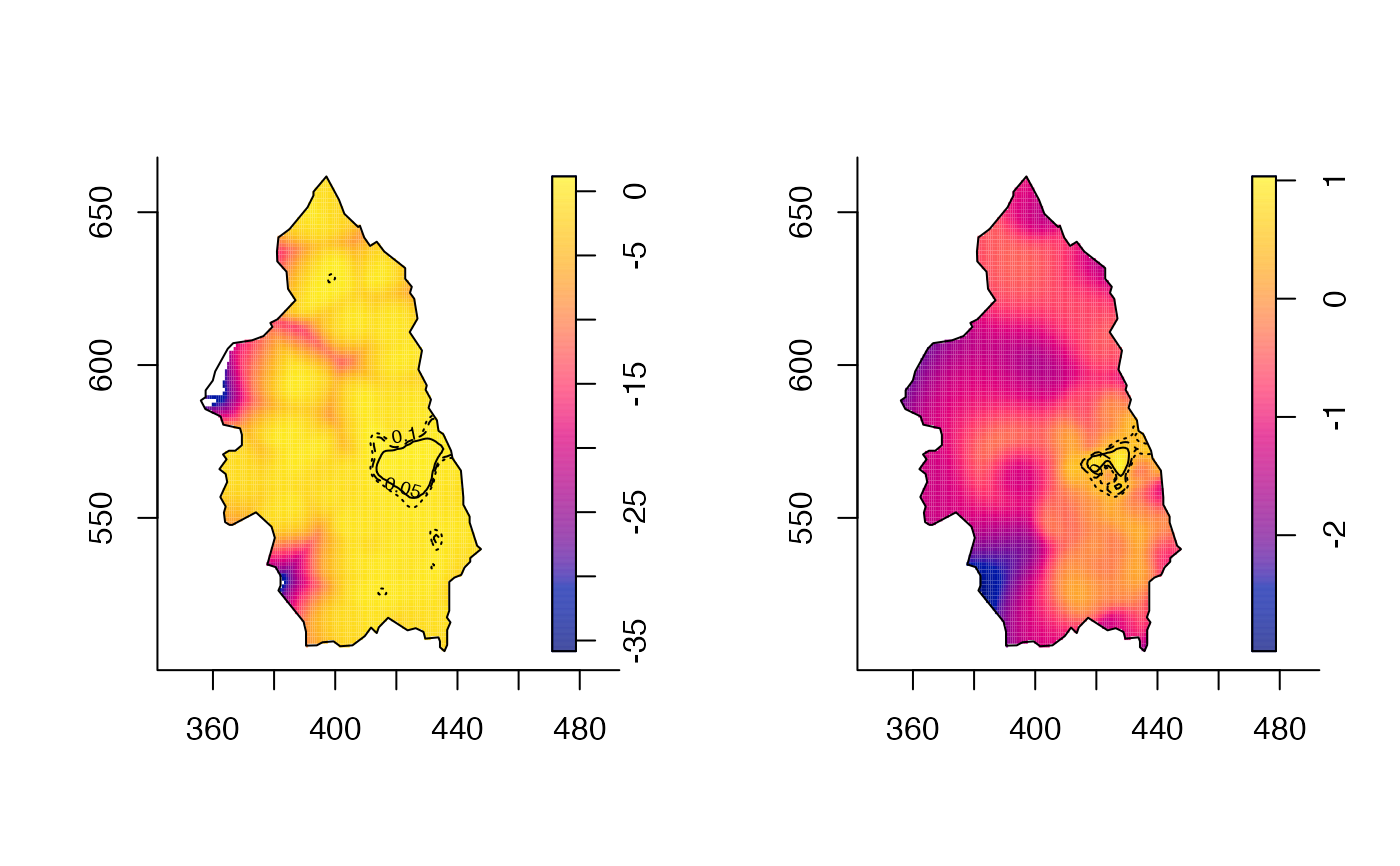
par(mfrow=c(1,2))
plot(riskfix)
tol.contour(fixtol1,levels=c(0.1,0.05,0.01),lty=3:1,add=TRUE)
plot(riskada)
tol.contour(adatol1,levels=c(0.1,0.05,0.01),lty=3:1,add=TRUE)
 # MC
fixtol2 <- tolerance(riskfix,method="MC",ITER=200)
#>
|
| | 0%
|
| | 1%
|
|= | 1%
|
|= | 2%
|
|== | 3%
|
|== | 4%
|
|=== | 4%
|
|=== | 5%
|
|==== | 5%
|
|==== | 6%
|
|===== | 7%
|
|===== | 8%
|
|====== | 8%
|
|====== | 9%
|
|======= | 10%
|
|======= | 11%
|
|======== | 11%
|
|======== | 12%
|
|========= | 13%
|
|========= | 14%
|
|========== | 14%
|
|========== | 15%
|
|=========== | 15%
|
|=========== | 16%
|
|============ | 17%
|
|============ | 18%
|
|============= | 18%
|
|============= | 19%
|
|============== | 20%
|
|============== | 21%
|
|=============== | 21%
|
|=============== | 22%
|
|================ | 23%
|
|================= | 24%
|
|================= | 25%
|
|================== | 25%
|
|================== | 26%
|
|=================== | 27%
|
|=================== | 28%
|
|==================== | 28%
|
|==================== | 29%
|
|===================== | 30%
|
|===================== | 31%
|
|====================== | 31%
|
|====================== | 32%
|
|======================= | 32%
|
|======================= | 33%
|
|======================== | 34%
|
|======================== | 35%
|
|========================= | 35%
|
|========================= | 36%
|
|========================== | 37%
|
|========================== | 38%
|
|=========================== | 38%
|
|=========================== | 39%
|
|============================ | 40%
|
|============================ | 41%
|
|============================= | 41%
|
|============================= | 42%
|
|============================== | 42%
|
|============================== | 43%
|
|=============================== | 44%
|
|=============================== | 45%
|
|================================ | 45%
|
|================================ | 46%
|
|================================= | 47%
|
|================================= | 48%
|
|================================== | 48%
|
|================================== | 49%
|
|=================================== | 50%
|
|==================================== | 51%
|
|==================================== | 52%
|
|===================================== | 52%
|
|===================================== | 53%
|
|====================================== | 54%
|
|====================================== | 55%
|
|======================================= | 55%
|
|======================================= | 56%
|
|======================================== | 57%
|
|======================================== | 58%
|
|========================================= | 58%
|
|========================================= | 59%
|
|========================================== | 59%
|
|========================================== | 60%
|
|=========================================== | 61%
|
|=========================================== | 62%
|
|============================================ | 62%
|
|============================================ | 63%
|
|============================================= | 64%
|
|============================================= | 65%
|
|============================================== | 65%
|
|============================================== | 66%
|
|=============================================== | 67%
|
|=============================================== | 68%
|
|================================================ | 68%
|
|================================================ | 69%
|
|================================================= | 69%
|
|================================================= | 70%
|
|================================================== | 71%
|
|================================================== | 72%
|
|=================================================== | 72%
|
|=================================================== | 73%
|
|==================================================== | 74%
|
|==================================================== | 75%
|
|===================================================== | 75%
|
|===================================================== | 76%
|
|====================================================== | 77%
|
|======================================================= | 78%
|
|======================================================= | 79%
|
|======================================================== | 79%
|
|======================================================== | 80%
|
|========================================================= | 81%
|
|========================================================= | 82%
|
|========================================================== | 82%
|
|========================================================== | 83%
|
|=========================================================== | 84%
|
|=========================================================== | 85%
|
|============================================================ | 85%
|
|============================================================ | 86%
|
|============================================================= | 86%
|
|============================================================= | 87%
|
|============================================================== | 88%
|
|============================================================== | 89%
|
|=============================================================== | 89%
|
|=============================================================== | 90%
|
|================================================================ | 91%
|
|================================================================ | 92%
|
|================================================================= | 92%
|
|================================================================= | 93%
|
|================================================================== | 94%
|
|================================================================== | 95%
|
|=================================================================== | 95%
|
|=================================================================== | 96%
|
|==================================================================== | 96%
|
|==================================================================== | 97%
|
|===================================================================== | 98%
|
|===================================================================== | 99%
|
|======================================================================| 99%
|
|======================================================================| 100%
adatol2 <- tolerance(riskada,method="MC",ITER=200,parallelise=2) # ~90secs with parallelisation
#> Running MC iterations on 2 / 16 cores...Done.
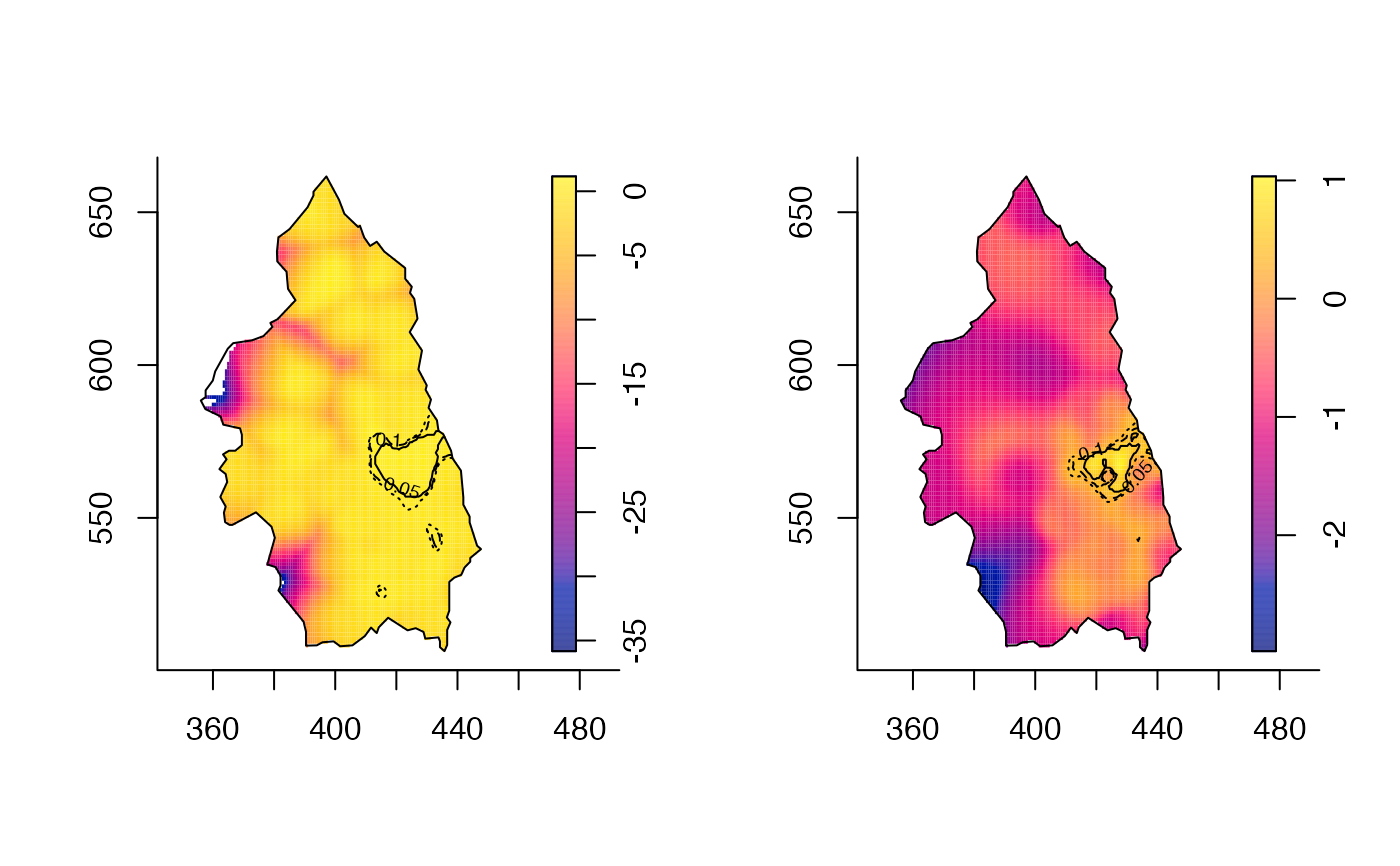
par(mfrow=c(1,2))
plot(riskfix)
tol.contour(fixtol2,levels=c(0.1,0.05,0.01),lty=3:1,add=TRUE)
plot(riskada)
tol.contour(adatol2,levels=c(0.1,0.05,0.01),lty=3:1,add=TRUE)
# MC
fixtol2 <- tolerance(riskfix,method="MC",ITER=200)
#>
|
| | 0%
|
| | 1%
|
|= | 1%
|
|= | 2%
|
|== | 3%
|
|== | 4%
|
|=== | 4%
|
|=== | 5%
|
|==== | 5%
|
|==== | 6%
|
|===== | 7%
|
|===== | 8%
|
|====== | 8%
|
|====== | 9%
|
|======= | 10%
|
|======= | 11%
|
|======== | 11%
|
|======== | 12%
|
|========= | 13%
|
|========= | 14%
|
|========== | 14%
|
|========== | 15%
|
|=========== | 15%
|
|=========== | 16%
|
|============ | 17%
|
|============ | 18%
|
|============= | 18%
|
|============= | 19%
|
|============== | 20%
|
|============== | 21%
|
|=============== | 21%
|
|=============== | 22%
|
|================ | 23%
|
|================= | 24%
|
|================= | 25%
|
|================== | 25%
|
|================== | 26%
|
|=================== | 27%
|
|=================== | 28%
|
|==================== | 28%
|
|==================== | 29%
|
|===================== | 30%
|
|===================== | 31%
|
|====================== | 31%
|
|====================== | 32%
|
|======================= | 32%
|
|======================= | 33%
|
|======================== | 34%
|
|======================== | 35%
|
|========================= | 35%
|
|========================= | 36%
|
|========================== | 37%
|
|========================== | 38%
|
|=========================== | 38%
|
|=========================== | 39%
|
|============================ | 40%
|
|============================ | 41%
|
|============================= | 41%
|
|============================= | 42%
|
|============================== | 42%
|
|============================== | 43%
|
|=============================== | 44%
|
|=============================== | 45%
|
|================================ | 45%
|
|================================ | 46%
|
|================================= | 47%
|
|================================= | 48%
|
|================================== | 48%
|
|================================== | 49%
|
|=================================== | 50%
|
|==================================== | 51%
|
|==================================== | 52%
|
|===================================== | 52%
|
|===================================== | 53%
|
|====================================== | 54%
|
|====================================== | 55%
|
|======================================= | 55%
|
|======================================= | 56%
|
|======================================== | 57%
|
|======================================== | 58%
|
|========================================= | 58%
|
|========================================= | 59%
|
|========================================== | 59%
|
|========================================== | 60%
|
|=========================================== | 61%
|
|=========================================== | 62%
|
|============================================ | 62%
|
|============================================ | 63%
|
|============================================= | 64%
|
|============================================= | 65%
|
|============================================== | 65%
|
|============================================== | 66%
|
|=============================================== | 67%
|
|=============================================== | 68%
|
|================================================ | 68%
|
|================================================ | 69%
|
|================================================= | 69%
|
|================================================= | 70%
|
|================================================== | 71%
|
|================================================== | 72%
|
|=================================================== | 72%
|
|=================================================== | 73%
|
|==================================================== | 74%
|
|==================================================== | 75%
|
|===================================================== | 75%
|
|===================================================== | 76%
|
|====================================================== | 77%
|
|======================================================= | 78%
|
|======================================================= | 79%
|
|======================================================== | 79%
|
|======================================================== | 80%
|
|========================================================= | 81%
|
|========================================================= | 82%
|
|========================================================== | 82%
|
|========================================================== | 83%
|
|=========================================================== | 84%
|
|=========================================================== | 85%
|
|============================================================ | 85%
|
|============================================================ | 86%
|
|============================================================= | 86%
|
|============================================================= | 87%
|
|============================================================== | 88%
|
|============================================================== | 89%
|
|=============================================================== | 89%
|
|=============================================================== | 90%
|
|================================================================ | 91%
|
|================================================================ | 92%
|
|================================================================= | 92%
|
|================================================================= | 93%
|
|================================================================== | 94%
|
|================================================================== | 95%
|
|=================================================================== | 95%
|
|=================================================================== | 96%
|
|==================================================================== | 96%
|
|==================================================================== | 97%
|
|===================================================================== | 98%
|
|===================================================================== | 99%
|
|======================================================================| 99%
|
|======================================================================| 100%
adatol2 <- tolerance(riskada,method="MC",ITER=200,parallelise=2) # ~90secs with parallelisation
#> Running MC iterations on 2 / 16 cores...Done.
par(mfrow=c(1,2))
plot(riskfix)
tol.contour(fixtol2,levels=c(0.1,0.05,0.01),lty=3:1,add=TRUE)
plot(riskada)
tol.contour(adatol2,levels=c(0.1,0.05,0.01),lty=3:1,add=TRUE)
 # }
# }